
Let’s quickly go over what each of these variables are.
Projectile equations full#
The \(x\) and \(y\) position changes along the path, with \(x_0\) and \(y_0\) marking the starting point.įor every projectile motion problem we’ll have a set of variables in each direction. Studying projectile motion allows for full application of kinematics, various equations of kinematic-motion and vector geometry. This is because the motion in the \(x\) and \(y\) components are independent of each other.įor example, at every point along the path of motion here, there is a velocity in the \(x\) direction and a velocity in the \(y\) direction. When we’re working with projectile motion, we are dealing with vectors like velocity and acceleration, which we break up into the \(x\) and \(y\) components. You’ll want to determine your starting point, end point, and the path of travel. Even an approximation can be helpful in visualizing the situation.
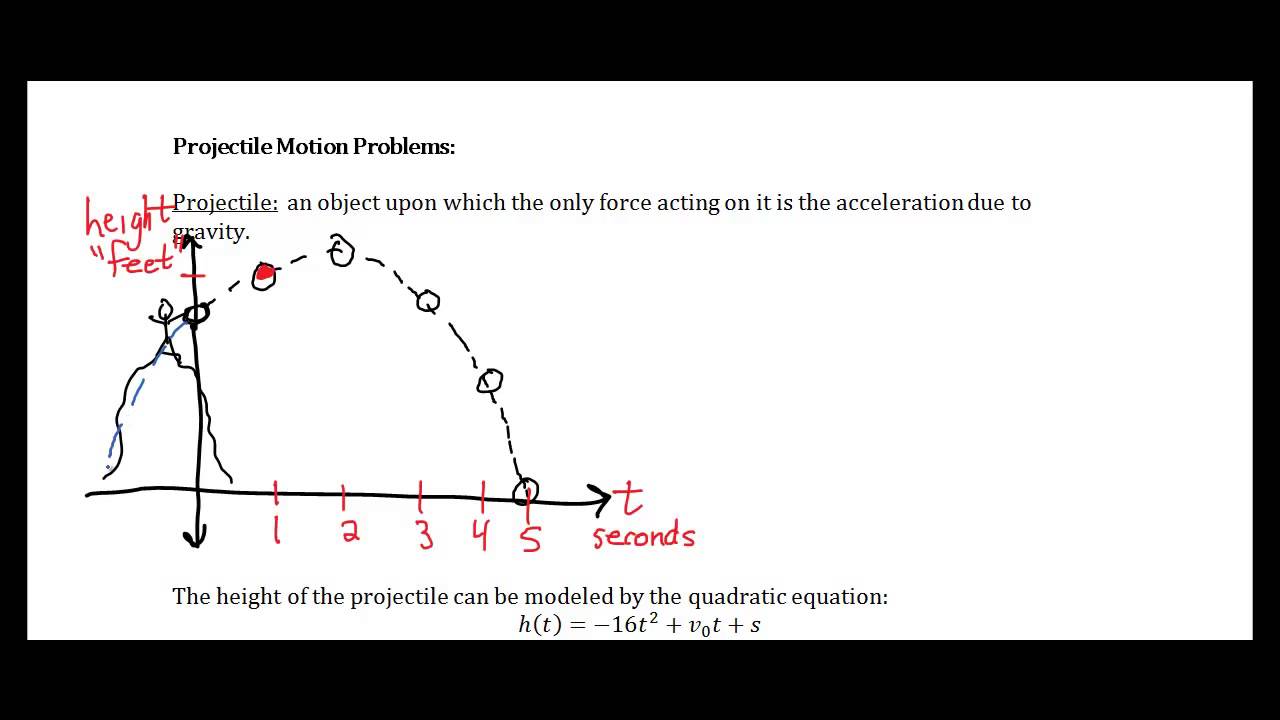
Since these two components of motion are independent of each other, two distinctly separate sets of equations are needed - one for the projectiles horizontal motion and one for its vertical motion. Is all of the motion vertical, like an object falling to the ground? Or is the object launched or thrown at some angle? It helps to draw out the trajectory if it isn’t already given to you. The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions - both horizontally and vertically. In other words, consider the direction the object is moving. When you begin a projectile motion problem, the first thing you’ll have to do is think about the trajectory of the object. Our ability to predict these values depends on the information we have about the scenario. With physics, it’s possible to predict things like where the object will land and the amount of time it will take for the object to reach the ground. We can view the motion of the projectile as a superposition of two motions, a. Projectile motion occurs any time an object is thrown or launched into the air and falls back to the ground. The position of a projectile as a function of time is given by r v0t + gt2. The velocity vector, v, is the red arrow: Taking off at an angle theta The initial velocity in.
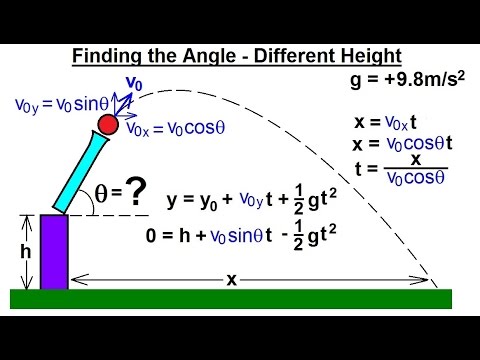
Hi, and welcome to this video on projectile motion! Today, we’ll discuss what projectile motion is and break down some important concepts. To use our projectile motion equations, we need the initial velocity in both the x and y directions.


 0 kommentar(er)
0 kommentar(er)
